阅读“flow-field-pathfinding”源码的研究笔记

简介

教程地址：https://howtorts.github.io/

---

常用结构

Vector2

构造函数和静态属性

名称	类型	作用
Vector2(x, y)	构造函数	创建一个二维向量对象，包含x和y坐标
Vector2.zero	静态属性	预定义的零向量 (0, 0)
Vector2.one	静态属性	预定义的单位向量 (1, 1)

Vector2实例方法

方法名	参数	返回值	作用
length()	无	Number	计算向量的长度（模长），等于到原点的距离
distanceTo(target)	Vector2	Number	计算当前向量到目标向量的欧几里得距离
normalize()	无	Vector2	返回当前向量的单位向量（方向相同，长度为1）
round()	无	Vector2	返回坐标四舍五入后的新向量
floor()	无	Vector2	返回坐标向下取整后的新向量
minus(other)	Vector2	Vector2	向量减法，返回两向量相减的结果
plus(other)	Vector2	Vector2	向量加法，返回两向量相加的结果
mul(scalar)	Number	Vector2	向量数乘，返回向量与标量相乘的结果
div(scalar)	Number	Vector2	向量除法，返回向量除以标量的结果
angle()	无	Number	返回向量的角度（以度为单位，相对于Y轴正方向）

工厂函数

函数名	参数	返回值	作用
vector2(x, y)	Array/Vector2	Vector2	工厂方法，可接受数组或Vector2对象，返回Vector2实例

相关辅助类

类名	构造参数	主要方法	作用
LineSegment	start, end	interpolatedPoint(percent)	表示线段，可进行插值计算
LineString	points数组	无	表示由多个点组成的折线，包含多个线段

注意：所有返回Vector2的方法都会创建新的向量对象，不会修改原向量（不可变性设计）。

Agent

构造函数

名称	参数	作用
Agent(pos)	pos (Vector2)	创建一个智能体对象，设置初始位置

Agent属性

属性名	类型	默认值	作用
position	Vector2	构造参数pos	智能体当前位置坐标
rotation	Number	0	智能体当前旋转角度
velocity	Vector2	Vector2.zero	智能体当前速度向量
maxForce	Number	5	最大加速度（这里假设单位质量为1，因此用力表示）
maxSpeed	Number	4	最大速度限制（网格单位/秒）

---

follow a path

教程
源码

这个用例比较简单，主要是讲述角色沿着固定路径移动。

//game tick
//敌人移动
for (var i = enemies.length - 1; i >= 0; i--) {
  var e = enemies[i];

  var distanceToMove = dt * e.speed; // 计算在当前时间间隔内敌人应移动的距离
  var vectorToTarget = path[e.pathIndex].minus(e.position); // 计算到下一个路径点的向量
  var distanceToTarget = vectorToTarget.length(); // 计算到下一个路径点的距离

  // 如果敌人在当前时间间隔内可以到达下一个路径点
  if (distanceToTarget < distanceToMove) {
    e.position = path[e.pathIndex]; // 将敌人移动到下一个路径点
    e.pathIndex++; // 更新路径索引

    // 如果敌人到达路径终点
    if (e.pathIndex == path.length) {
      enemies.splice(i, 1); // 从敌人数组中移除该敌人
      continue;
    }

    // 重新计算到下一个路径点的移动距离和向量
    distanceToMove -= distanceToTarget;
    vectorToTarget = path[e.pathIndex].minus(e.position);
    distanceToTarget = vectorToTarget.length();
  }

  // 更新敌人的位置和旋转角度
  e.position = e.position.plus(vectorToTarget.normalize().mul(distanceToMove));
  e.rotation = vectorToTarget.angle();
}

---

Generating a path with Dijkstra

教程
源码

这个教程主要讲述如何使用Dijkstra生成路径：

1. 先使用广度优先搜索（BFS）来生成Dijkstra网格
2. 然后根据Dijkstra从起点开始生成移动路径
3. 最后再使用上一篇文章的路径移动方案来控制敌人移动

生成Dijkstra网格:

1. 将所有网格的权重改为空，表示未访问。
2. 再将所有塔的网格权重改为Number最大值，表示为不可达。
3. 将终点权重设置为0，然后放入到待访问列表。
4. 每次从待访问列表里拿出节点（教程用了列表，BFS常见还是用队列比较好）。
5. 遍历节点的四个方向邻居。
6. 如果邻居节点未访问过，则设置其权重值为当前节点权重+1，并将邻居节点放入待访问列表。
7. 重复执行4、5、6，直到待访问列表为空。

权重值就是节点到终点的曼哈顿距离。

最后可得到整个网格所有节点到终点的距离（权重）。以下为教程源码：

function generateDijkstraGrid() {
	// 生成一个空网格，所有位置的权重设置为 null（表示未访问）
	dijkstraGrid = new Array(gridWidth);
	for (var x = 0; x < gridWidth; x++) {
		var arr = new Array(gridHeight);
		for (var y = 0; y < gridHeight; y++) {
			arr[y] = null;
		}
		dijkstraGrid[x] = arr;
	}

	// 将塔的位置设置为权重 MAXINT（表示无法通过）
	for (var i = 0; i < towers.length; i++) {
		var t = towers[i];
		dijkstraGrid[t.x][t.y] = Number.MAX_VALUE;
	}

	// 从终点开始进行洪水填充
	pathEnd.distance = 0;
	dijkstraGrid[pathEnd.x][pathEnd.y] = 0;

	var toVisit = [pathEnd]; // 待访问节点队列

	// 遍历待访问节点
	for (i = 0; i < toVisit.length; i++) {
		var neighbours = neighboursOf(toVisit[i]); // 获取当前节点的邻居

		// 遍历邻居节点
		for (var j = 0; j < neighbours.length; j++) {
			var n = neighbours[j];

			// 如果邻居节点未访问过
			if (dijkstraGrid[n.x][n.y] === null) {
				n.distance = toVisit[i].distance + 1; // 设置权重
				dijkstraGrid[n.x][n.y] = n.distance;
				toVisit.push(n); // 加入待访问队列
			}
		}
	}
}

根据Dijkstra生成移动路径：

1. 判断起点是否为未访问或者不可达，如果是则直接返回。
2. 将起点放入到路径列表中，并将起点作为当前节点。
3. 获取当前节点的四个方向邻居节点。
4. 然后将最小权重的邻居节点放入路径列表中，并且作为下一个待访问节点。
5. 重复步骤3、4，知道当前节点等于终点。

最后可得到起点到终点的移动路径。以下为教程源码：

while (at.x != pathEnd.x || at.y != pathEnd.y) {
	currentWeight = dijkstraGrid[at.x][at.y];

	var neighbours = neighboursOf(at); // 获取当前位置的所有邻居节点
	var next = null; // 用于存储下一个要移动到的节点
	var nextWeight = currentWeight; // 初始化下一个节点的权重为当前权重

	// 遍历所有邻居节点
	for (var i = 0; i < neighbours.length; i++) {
		var neighbour = neighbours[i];
		var neighbourWeight = dijkstraGrid[neighbour.x][neighbour.y];

		// 如果邻居节点的权重小于当前权重
		if (neighbourWeight < nextWeight) {
			next = neighbour; // 更新下一个节点
			nextWeight = neighbourWeight; // 更新下一个节点的权重
		}
	}

	path.push(next); // 将下一个节点加入路径
	at = next; // 更新当前位置为下一个节点
}

---

Steering Behaviours Introduction

教程：Steering Behaviours Introduction
源码：3-1-steering-behaviours-seek
参考：The-Next-Vector-Improvements-in

RTS游戏有以下的特点，单位不会互相穿透，可以避开障碍，并且像一个群体一样移动。因此这里使用到Steering Behaviours（转向行为）

常见行为：

• Seek（寻找）：向固定点移动
• Flee（逃离）：远离固定点
• Pursue（追击）：预测实体的未来位置并寻求拦截它
• Evade（躲避）：预测实体的未来位置并逃跑避开它
• Avoidance（回避）：避免撞到东西

Seek转向行为：

function steeringBehaviourSeek(agent) {
  // 使用终点减智能体当前坐标，得出指向向量（desired）
  var desired = destination.minus(agent.position);

  // 最大速度除以
  desired = desired.mul(agent.maxSpeed / desired.length());

  // 期望速度 - 当前速度 = 需要改变的“速度差”
  var force = desired.minus(agent.velocity);

  // 把速度差转换成实际可施加的力（按最大推力比例缩放）
  return force.mul(agent.maxForce / agent.maxSpeed);
}

Seek公式：

$$ \begin{aligned} \vec{d} &= P_{dest} - P_{agent} \\\\ \vec{v}_{desired} &= \frac{\vec{d}}{|\vec{d}|} \cdot v_{max} \\\\ \vec{F} &= (\vec{v}_{desired} - \vec{v}_{agent}) \cdot \frac{F_{max}}{v_{max}} \\\\ \end{aligned} $$

其中

• $P_{dest}$：目标位置
• $P_{agent}$：智能体当前位置
• $\vec{d}$：智能体当前位置指向终点的向量。
• $v_{max}$：最大允许速度(量)
• $F_{max}$：最大允许推力(量)

最终返回的 $\vec{F}$ 就是施加在智能体上的转向力。

这里的公式与代码有一些差别：变量命名和公式顺序
首先就是desired，在代码里面是一个变量，但在公式里面分别是指向终点的向量：$\vec{d}$ 和指向终点的速度：$v_{max}$。
代码为了优化是先计算$\frac{v_{max}}{|\vec{d}|}$，实际上这里是先求$\vec{d}$单位向量，然后再乘最大速度来求期望速度。

最后一条公式比较晦涩，因为力除以速度没有任何物理意义。如果加上质量就很清晰了：

$$ \vec{F} = \vec{v}_{desired} - \vec{v}_{agent} $$ $$ \begin{aligned} F = ma \quad a = \frac{\Delta v}{\Delta t} \\\\ F = m\frac{\Delta v}{\Delta t} \\\\ \text{两边同除以} \Delta v\quad \frac{F}{\Delta v} = \frac{m}{\Delta t} \\\\ \end{aligned} $$ $$ \begin{aligned} \vec{F} &= (\vec{v}_{desired} - \vec{v}_{agent}) \cdot \frac{F_{max}}{v_{max}} \\\\ &= (\vec{v}_{desired} - \vec{v}_{agent}) \cdot \frac{m}{t} \\\\ &= \frac{\vec{v}_{desired} - \vec{v}_{agent}}{t} \cdot m \end{aligned} $$

这样就可以理解为最大推力使物体达到最大速度所使用的时间，让物体转向到期望速度所需要的推力。

移动智能体：

// game tick
// 遍历并移动所有智能体（从后向前，便于动态增删）
for (var i = agents.length - 1; i >= 0; i--) {
  var agent = agents[i];

  // 计算当前智能体的“寻找”行为力
  var seek = steeringBehaviourSeek(agent);

  // 将力施加到速度上（加速度积分）
  agent.velocity = agent.velocity.plus(seek.mul(dt));

  // 如果速度超过最大速度，则进行限速
  var speed = agent.velocity.length();
  if (speed > agent.maxSpeed) {
      agent.velocity = agent.velocity.mul(agent.maxSpeed / speed);
  }

  // 根据速度方向更新朝向角度
  agent.rotation = agent.velocity.angle();

  // 根据当前速度移动位置
  agent.position = agent.position.plus(agent.velocity.mul(dt));
}

这里获取到的seek其实就是seek返回的推力，由于忽略了质量（假设为1），因此后续计算直接乘以时间来获得推力方向的速度，最后再叠加到智能体当前速度，然后将最终速度限制在最大速度。

---

Steering Behaviours: Flocking

教程：Steering Behaviours: Flocking
源码：3-2-steering-behaviours-flock

群集行为是转向行为的一个子集，根据相邻智能体调整

群集行为：

• Separation（分离）：远离太过亲近的实体
• Cohesion（凝聚）：靠近那些我们靠近但不够近的实体
• Alignment（结盟）：改变方向，更加贴近邻居

Separation（分离）

实现代码：

function steeringBehaviourSeparation(agent) {
	var totalForce = Vector2.zero;
	var neighboursCount = 0;

	for (var i = 0; i < agents.length; i++) {
		var a = agents[i];
		if (a != agent) {
			var distance = agent.position.distanceTo(a.position);
			if (distance < agent.neighbourRadius && distance > 0) {
				//Vector to other agent
				var pushForce = agent.position.minus(a.position);
				//Inverse scaled force (bigger the nearer we are)
				pushForce = pushForce.normalize().mul(1 - (pushForce.length() / agent.neighbourRadius)); 
				totalForce = totalForce.plus(pushForce);
				neighboursCount++;
			}
		}
	}

	if (neighboursCount == 0) {
		return Vector2.zero;
	}

	totalForce = totalForce.div(neighboursCount);
	return totalForce.mul(agent.maxForce);
}

遍历所有智能体，然后挑选在生效半径内的邻居，求对应的分离力，最后将分离力求和。
最后需要除以生效邻居的数量进行平均，最后再乘以力的最大值得到最后的分离力。

Separation公式：

$$ \begin{aligned} \vec{d} &= \vec{p}_{\text{agent}} - \vec{p}_{\text{neighbour}} \\ {scale} &= 1 - \frac{|\vec{d}|}{r_\text{neighbour}} \\ \vec{F}_{\text{push}} &= \frac{\vec{d}}{|\vec{d}|} \cdot {scale} \\ \vec{F}_{\text{total}} &= \vec{F}_{\text{total}} + \vec{F}_{\text{push}} \end{aligned} $$

其中：

• $P_{agent}$：智能体当前位置
• $P_{neighbour}$：邻居当前位置
• $r_{neighbour}$：分离力的生效半径（内）
• $\vec{d}$：邻居指向智能体的向量。
• $scale$：根据距离计算的缩放量，距离越近，值越大
• $F_{push}$：当前邻居所产生的分离力
• $F_{total}$：所有邻居（在生效半径内）所产生的分离力

使用智能体和邻居获取分离力的单位方向，然后再根据距离和生效半径求分离力的比例来得到当前邻居产生的分离力。
后面就是平均分离力，然后再乘以$F_{max}$来得到最终的分离力

这里单个scale不会超过1的，所有的分离力平均下来也不会超过1，因此最终的分离力不会超过$F_{max}$

Cohesion（凝聚）

实现代码：

function steeringBehaviourCohesion(agent) {
	//Start with just our position
	var centerOfMass = agent.position;
	var neighboursCount = 1;

	for (var i = 0; i < agents.length; i++) {
		var a = agents[i];
		if (a != agent) {
			var distance = agent.position.distanceTo(a.position);
			if (distance < agent.neighbourRadius) {
				//sum up the position of our neighbours
				centerOfMass = centerOfMass.plus(a.position);
				neighboursCount++;
			}
		}
	}

	if (neighboursCount == 1) {
		return Vector2.zero;
	}

	//Get the average position of ourself and our neighbours
	centerOfMass = centerOfMass.div(neighboursCount);

	//seek that position
	return steeringBehaviourSeek(agent, centerOfMass);
}

遍历所有智能体，然后挑选在生效半径内的邻居，跟当前的智能体求一个平均的坐标位置作为聚集点，再使用之前提到的Seek对这个聚集点求吸引力。

Alignment（结盟）

结盟的运算跟凝聚类似，不过凝聚是智能体靠近邻居的平均位置。而结盟则是让智能体移动一致。

结盟代码：

function steeringBehaviourAlignment(agent) {
	var averageHeading = Vector2.zero;
	var neighboursCount = 0;

	//for each of our neighbours (including ourself)
	for (var i = 0; i < agents.length; i++) {
		var a = agents[i];
		var distance = agent.position.distanceTo(a.position);
		//That are within the max distance and are moving
		if (distance < agent.neighbourRadius && a.velocity.length() > 0) {
			//Sum up our headings
			averageHeading = averageHeading.plus(a.velocity.normalize());
			neighboursCount++;
		}
	}

	if (neighboursCount == 0) {
		return Vector2.zero;
	}

	//Divide to get the average heading
	averageHeading = averageHeading.div(neighboursCount);

	//Steer towards that heading
	var desired = averageHeading.mul(agent.maxSpeed);
	var force = desired.minus(agent.velocity);
	return force.mul(agent.maxForce / agent.maxSpeed);
}

遍历所有智能体，然后挑选在生效半径内的邻居，将邻居的速度方向想加求平均，得到一个结盟的期望速度方向，然后跟Seek一样，求出一个让智能体趋向于这个速度方向的推力。

---

叠加所有力

前面分别做了Seek（寻找）、Separation（分离）、Cohesion（凝聚）、Alignment（结盟）四种作用力的计算，现在需要把它作用到智能体中，计算出最终的速度和位置。

首先要对作用力的计算和位移分开成两次循环，这是因为位移会影响到作用力的计算，确保每个智能体都是基于一致的情况来做出行为。

求作用力的代码：

// game tick
// 遍历所有智能体

//Work out our behaviours
var seek = steeringBehaviourSeek(agent, destination);
var separation = steeringBehaviourSeparation(agent);
var cohesion = steeringBehaviourCohesion(agent);
var alignment = steeringBehaviourAlignment(agent);

//Combine them to come up with a total force to apply
agent.forceToApply = seek.plus(separation.mul(2)).plus(cohesion.mul(0.2)).plus(alignment.mul(0.5));

//Cap the force if required
if (agent.forceToApply.length() > agent.maxForce) {
  agent.forceToApply = agent.forceToApply.normalize().mul(agent.maxForce);
}

作者并没有把所有的力直接相加，这是因为这些作用力是有优先级的：例如凝聚中靠前面的智能体会有一个凝聚力向后拉扯，有可能导致它或者队伍没法达到最高速度。这种情况下，凝聚力的作用反而产生负面影响，所以作者的做法是对不同作用力加权相加，像凝聚力只需要少量，让队伍不至于分散就行。

接下来的循环跟之前一样，计算作用力产生的加速度，然后计算出智能体最新的位置、旋转即可。

---

优化

作者谈到几个问题和优化的方向：

• 凝聚和结盟会让不同终点的单位互相拉扯，导致没法正确最快到达终点。可以只对相似终点的单位进行凝聚和结盟。（作者使用了相似，但这个相似是相对的，离终点越近，相似的阈值应该越低，这个参数并不好调）
• 重复遍历了智能体多次，时间复杂度较高，可以使用四叉树等空间搜索方法来优化。（这是常见的降时间复杂度方案了）
• 另外就是从频次入手去减少遍历智能体的耗时，某些转向行为重要性并不是特别高，所以实时性也可以相应降低，可以通过分帧处理来优化，没有计算的帧使用之前缓存。

除了上述所说的，其实还有其他一些优化方向：

• 上述的群聚行为，其实都是基于相同范围内的邻居，那其实可以预计算出邻居列表，然后再分发到每个转向行为进行计算。
• 作者的部分公式实现没有进一步优化，例如不直接用distanceTo计算距离来进行对比，变成计算距离的平方进行对比，这样少开一次根号了，后续也能直接使用向量。
• 计算分离力时，用的是线性函数。这里换成二次函数一样也能达到目的（分离力会更强，需要在后续适当降低权重）。这样的好处也是减少开根号。

---

Flow Fields: Line of Sight

教程：Flow Fields: Line of Sight
源码：9-flow-field-improvements-again

原文说明

在流场寻路的基础上，增加视野的定义。用于解决“明明直线就可以到达终点，但移动却是曲线”的问题。

作者的处理方法是通过判断当前的节点是否拥有终点的视野（节点到终点中间没有阻挡）。原文作者的思路如下：

1. 终点肯定是拥有视野的。
2. 终点的（垂直、水平）直线邻居，也是拥有视野的（非阻挡）。
3. 如果节点跟终点是一条（垂直、水平）直线上的，而更靠近终点的下一个节点有视野，那它也有视野。

这里原文描述的有点绕，简单点就是直线节点和终点之间没有阻挡，则有视野

4. 如果朝向终点最有影响力的方向节点有视野，并且朝向终点的对角线有视野，那它也有视野

4是原文最难理解的，要说明白，要把两个定义拆开来说：朝向终点最有影响力的方向节点、朝向终点的对角线

朝向终点最优影响力的方向节点：

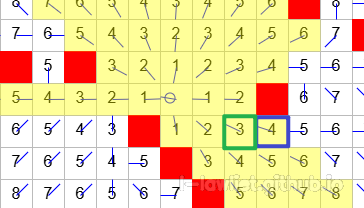
上图的蓝色框节点就是当前节点。左右上下四个节点都是它的方向节点，那么哪个方向节点对它朝向终点最有影响力的呢？首先可以排除右下两个，因为他们不是朝向终点的。
剩下左和上两个，最终判定是有视野的，那么上方的阻断并不是最优影响力的，而是左边节点。这里其实可以通过当前节点指向终点的射线来理解，射线方向其实更偏向左边，所以左边是否为有视野对当前节点影响最大。所以左边拥有视野，它也可能拥有视野。

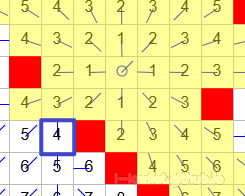
如上图，如果射线方向是指向对角线（右上角）呢？那对角线隔壁的两个方向节点都拥有相同的影响力，那么两个只要一个拥有视野，它也可能拥有视野。
这里还要补充一个代码里面有，但没有说明的情况：这两个方向节点都不能为阻挡，因为视野是平分的，有一个为阻挡则表现智能体有一半穿过阻挡节点的角

• 朝向终点的对角线：
  

  

  
  

  

还是上面的两个图片来解释另外一个必须的条件。朝向终点的对角线其实比较容易理解，就是射线指向的那个对角线。而这个对角线拥有视野，则说明这个对角线前面也是一览无遗的，那么才能确保它是拥有视野的。

实现代码：

function calculateLos(at, pathEnd) {
	var xDif = pathEnd.x - at.x;
	var yDif = pathEnd.y - at.y;

	var xDifAbs = Math.abs(xDif);
	var yDifAbs = Math.abs(yDif);

	var hasLos = false;

	var xDifOne = Math.sign(xDif);
	var yDifOne = Math.sign(yDif);

	//Check the direction we are furtherest from the destination on (or both if equal)
	// If it has LOS then we might

	//Check in the x direction
	if (xDifAbs >= yDifAbs) {

		if (losGrid[at.x + xDifOne][at.y]) {
			hasLos = true;
		}
	}
	//Check in the y direction
	if (yDifAbs >= xDifAbs) {

		if (losGrid[at.x][at.y + yDifOne]) {
			hasLos = true;
		}
	}

	//If we are not a straight line vertically/horizontally to the exit
	if (yDifAbs > 0 && xDifAbs > 0) {
		//If the diagonal doesn't have LOS, we don't
		if (!losGrid[at.x + xDifOne][at.y + yDifOne]) {
			hasLos = false;
		} else if (yDifAbs === xDifAbs) {
			//If we are an exact diagonal and either straight direction is a wall, we don't have LOS
			if (dijkstraGrid[at.x + xDifOne][at.y] === Number.MAX_VALUE || dijkstraGrid[at.x][at.y + yDifOne] === Number.MAX_VALUE) {
				hasLos = false;
			}
		}
	}
	//It's a definite now
	losGrid[at.x][at.y] = hasLos;

	//TODO: Could replace our distance with a direct distance?
	// Might not be worth it, would need to use a priority queue for the open list.
}

这里代码实现的比较巧妙：

• 首先获取节点相对终点的横向、纵向距离和单位方向。
• 通过横向、纵向距离和单位方向判断出哪个方向节点是对当前节点影响最大的，通过方向节点的视野推出当前节点的视野。
• 如果不是终点，那接着就是对一些不满足的情况取消视野。
  • 如果对角线没有视野，则取消其视野。（不满足“朝向终点的对角线有视野”条件）
  • 如果横向、纵向距离都相同，则需要判断两个方向节点是否都是非阻挡，有一个为阻挡则取消其视野。（方向节点平分了视野，需要同时为非阻挡）

接着就是在遍历Dijkstra网格时，把视野处理也加上（遍历Dijkstra网格的顺序符合视野的处理顺序，都是从终点开始广度搜索）

补充说明

“如果朝向终点最有影响力的方向节点有视野，并且朝向终点的对角线有视野，那它也有视野”这条规则其实被作者简化了很多，在特殊情况下，这两个必要条件有可能不满足也有视野。

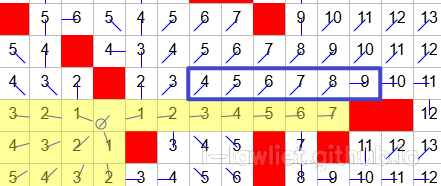
例如上图蓝框部分，即使方向节点丢失视野，但它仍然可以拥有视野，这是由于前面的方向节点都受到终点上方的阻挡影响，导致都失去了视野。

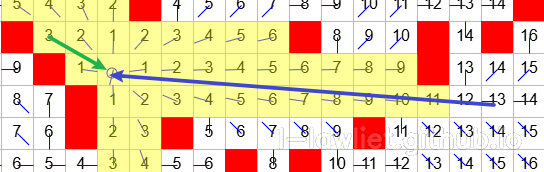
另外一种特殊情况，即使对角线没视野，但它仍然可以拥有视野，例如射线趋近于方向节点时，尽管对角线没有视野，也不能证明它没有视野。例如下图节点12、13（蓝色箭头开始位置）受到的阻挡远远小于节点3（绿色箭头开始位置），但由于这个条件导致丢失视野。

---